磁場の距離減衰について

大雑把なイメージとして、起磁力を大きな磁石に例えれば、距離減衰の仕方は、その長さ(磁気モーメントの長さ)に依存します。

磁気モーメントが長いと、距離減衰は緩やかに、短いと急激になります。

磁気モーメントは、N極とS極の2つの磁荷面(磁石の太さあり)です。
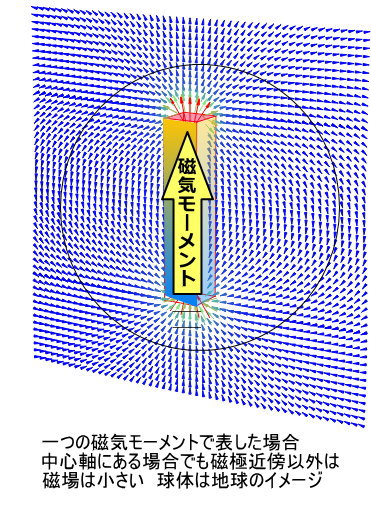
もう少し正確に電流といった形で、表現する場合は、円電流を束ねたコイルをイメージになります。

もちろん、これらは、あくまで全てイメージとして考える場合で、Qmは、超伝導コイルを(離散化された)立体電流で計算しています。

上記を数式として定量的に表現すれば

電場磁場の距離減衰については、その源の形状に大きく依存します。

（1）点源については、クーロンの法則で知られていますように、距離の逆二乗に比例します
\[H=C\dfrac{m}{r^2}\]
\(H:磁場　m:磁荷　r:距離　C:比例定数\)

（2）無限長線源については、アンペールの法則が示すように距離に反比例します。
\[H=C\dfrac{ρ}{r}\]
ρ:線磁荷密度

アンペールの法則は電流ですが次のようになります。
\[H=\dfrac{I}{2πr}\]
I:電流

（3）無限に広い平板であれば、距離減衰はありません。
\[H=Cσ\]

\(σ:面磁荷密度\)

（4）有限長の線源の場合は、ビオサバールの法則があり、線源を見る角度をのファクターが入り(1)と(2)の中間となります。

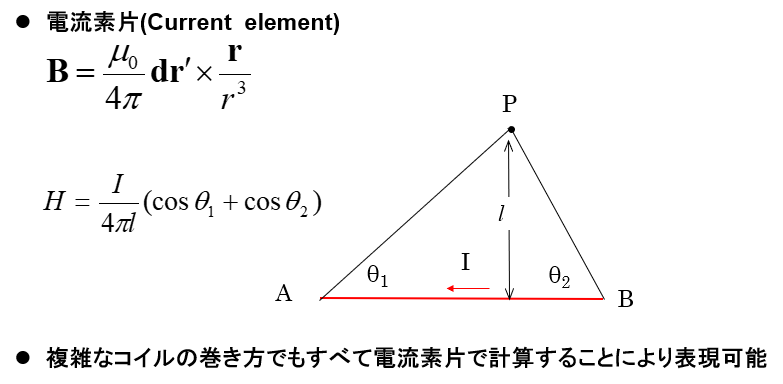
（5）曲面Sの源であると積分にした形になります。　面磁荷密度が一定の場合、(2)と(3)の間で立体角Ωに比例します。

\[H=CΩ\]

\[Ω=\iint_s \dfrac{dS(r ,n)}{r^3}dr\]

これらはすべて3次元空間上における保存則からくるもので、純粋に幾何学(数学)になります。