第一部 何故 3次元磁場解析はQmが有利なのか!
FEM系のソフトとの違いについて、理論を交えてのもう少し詳しい説明します。 長文になりますので複数に分けて解説します。
概要
3次元リアルタイム磁場解析ソルバーQmとは
- 非線形3次元動磁場解析のRADツールです。
- 運動及び渦電流(非線形磁性体を含む)を含めた解析ソルバです。
- 空間メッシュ・境界条件不要の積分方程式法を採用しています。
- 磁性体部分は面変数型の磁気モーメント法により少ない分割で高精度を実現しています。
広範囲な産業と応用分野
汎用磁場解析ソフトであるので広範囲の産業で利用されています。
→基本的に電気または磁石を利用するところではすべて関係します。
→電気・電子・精密・機械・土木・建設・自動車・原子力・エネルギー・環境・資源探査・医学,etc…
- キーワード: 渦電流・電磁石・永久磁石・電磁誘導
永久磁石製品、永久磁石製作、着磁器、磁気特性計測
リレー、プランジャ、スイッチング機器
モータ類、ステッピングモータ、ボイスコイルモータ、リニアモータ、
各種電磁石設計、Qレンズ、偏向ヨーク - MRI、シールドルーム、電磁気器の磁気シールド
- 磁気浮上、磁気軸受け、宙に浮く独楽、電磁カップリング
- 磁気センサ、金属探知機、磁気探勝、資源探査
特長
モデルの違いから見る特長
Qmは空間メッシュ不要でモデル作成を省力化
- 面倒なメッシュ分割が不要でモデル作成が省力化できます。
- 動きを伴うもの・相互位置関係が変わるパラメータサーベイには有利です。
→相互位置関係からみた解析値の連続性の保証されます。
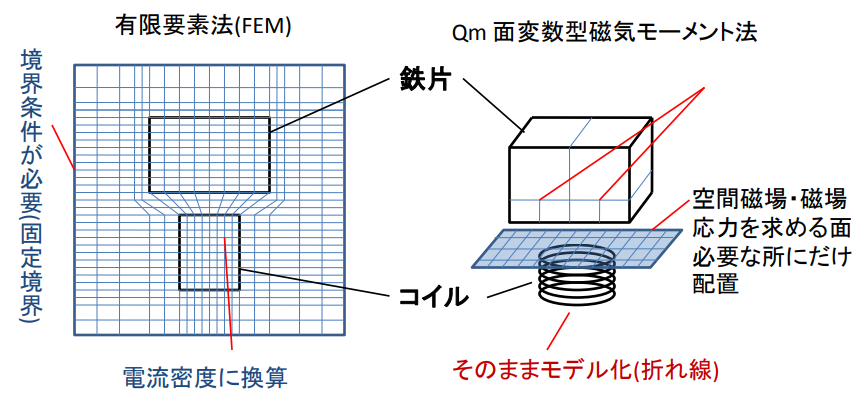
FEM磁場解析理論
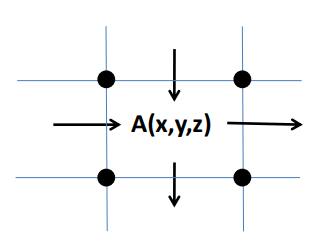
空間も含めベクトルポテンシャルAは周りの節点の値で補完できると仮定します。 ※形状関数・補完関数と呼ばれます。

要素への出入りのバランス式を立てます。
※エネルギー最小などの条件があります。

漸化式となり境界条件を与えます。 式を連立一次方程式として構築するとバンドマトリックスとなります。
したがって要素内の磁場の値は周りの4点の値の補完値となりメッシュを細かくしない限り精度は上がりません。
辺に変数を置くFEMもあるが補完値であることは変わりません。

その特性から、急激な変化に対してはメッシュを細分化するしかなくなります。
また、物理現象として考えても、磁性体やコイルの形・寸法・物性に関係のない空間部分のメッシュ分割により解が変化するという離散化による安定性・一貫性のない現象が生じます。
※FEMは、構造解析のように場の変数が初等関数表現できる場合には、分割のよる離散化誤差は生じにくいが(変分原理)、磁場の変数は超越関数ですので、分割による影響を受けやすくなります。 控えめに言っても、少なくとも、磁場の解を表現する手法として適切ではありません。
Qm磁場解析理論(面変数の改良型磁気モーメント法)
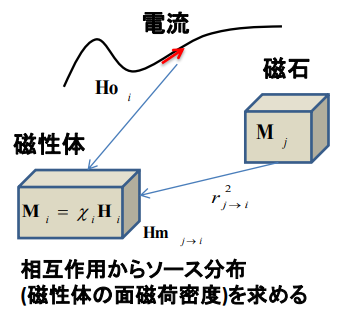
空間及び磁性体内部も含めて任意場所の磁場\(\textbf{H}(x, y, z)\)は重ね合わせの原理から
\(\begin{equation}
\mathbf{H} = \mathbf{Ho} + \mathbf{Hm}\tag{1}
\end{equation}\)
\(i\)番目の磁性体では
\(\begin{equation}
\mathbf{H}_i = \mathbf{Ho}_i + {\mathbf{Hm}_i}\tag{2}
\end{equation}\)
\(\mathbf{Ho}_i\): \(i\)番目の磁性体への電流等からの寄与です。 ビオサバールの法則
\(\mathbf{Hm}_i\): \(i\)番目の磁性体への磁性体からの寄与です。
\(\mathbf{Hm}\)は、磁性体に発生した磁気モーメントの分布\(\mathbf{M}(r)\)と距離\(r\)が分かれば クーロンの磁場の法則で求まります。
\(\begin{equation}
\mathbf{Hm} = -\dfrac{1}{4\pi}\int_v\nabla\dfrac{\mathbf{M}(r)\cdot\mathbf{r}}{r^3}dv\tag{3}
\end{equation}\)
\(\mathbf{M}\)が磁性体面毎に一定とすると、\(i\)番目の面に対して離散化した式は
\(\begin{equation}
\mathbf{Hm}_i = -\dfrac{1}{4\pi}\sum_j\dfrac{\mathbf{M}_j}{r^2_{j{\rightarrow}i}}\tag{4}
\end{equation}\)
となります。
また、各磁性体で磁化率\(\chi\)に対して
\(\begin{equation}
\mathbf{M}_i = \chi_i\mathbf{H}_i\tag{5}
\end{equation}\)
が成立するのでこの式に(2)式,(4)式を代入すると
\(\begin{equation}
\dfrac{\mathbf{M}_i}{\chi_i} = \mathbf{Ho}_i-\dfrac{1}{4\pi}\sum_j\dfrac{\mathbf{M}_j}{r^2_{j{\rightarrow}i}}\tag{6}
\end{equation}\)
が得られ を未知数する連立一次方程式として解くことができます。
また、磁性体をセルに分割して磁化率\(\chi_i\) を反復修正することにより非線形計算を扱うことができます。
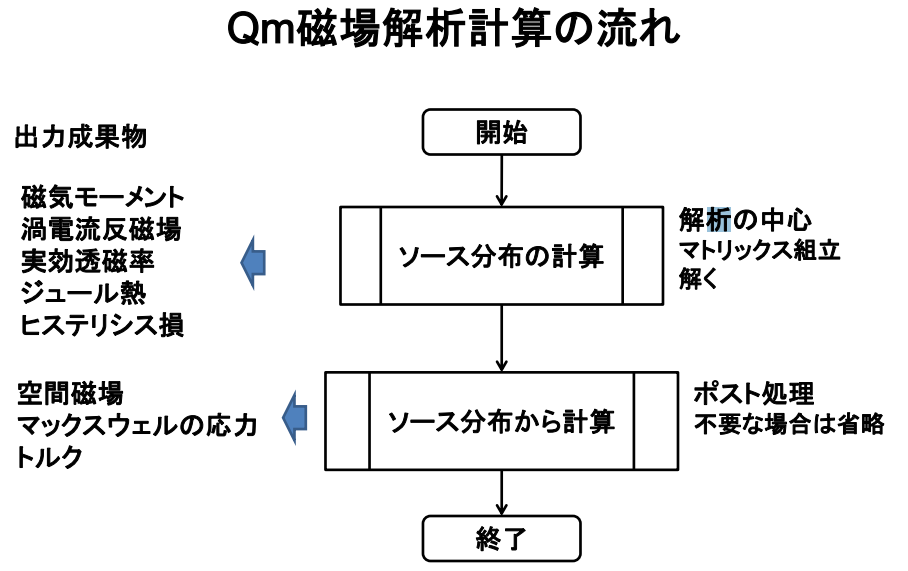
Qm磁場解析計算の流れ
Qmは、次の二段階で計算します。
(1)磁性体相互作用から、磁場の源の分布を連立1次方程式(非線形計算の場合はイタレーションします)で解きます。
(2)磁場の源の分布が分れば解析式で任意の場所の磁束密度を計算します。
空間メッシュのないQmのメリット
- 空間メッシュがないから・・・
→変数の数が少ないので計算が高速
特に広い解析空間を有する問題 ・・・ 磁気シールド・薄型モータ
- 空間磁場は積分の解析解を利用するので高精度です。
→尖った形状磁性体が作る磁場の計算精度が高い
Qmは針状の磁性体・粗巻きコイル・ロータ、ステータの突起など空間で急激に変化する問題に強い
前述のFEM説明でも述べましたが、
→FEM系のソルバは磁場が急激に変化する空間もメッシュが必要なので微細なメッシュが必要です。
しかも、形状関数としてほとんど線形補間を過程しているので精度が悪くなります。
そもそも、空間磁場の関数は解析的に超越関数ですので、初等関数では表現できません。
- 運動のある問題も簡単に扱えます。
→動きによる空間メッシュの整合性は考えなくて良い。
- モデルが簡素になります。
→コイルと磁性体・導体だけのモデル化で計算できます。
→実験とよく似ているので直感的に扱えます。
実装機能としての特長
磁場解析のRADツール
- ソルバーに組み込まれたポスト
→カット&トライを繰り返すRADツールとして欠かすことの出来ない機能です。 - 計算中でもリアルタイムに可視化処理
→ソルバーとポスト部のメモリ共有とマルチスレッド機能によりリアルタイムに図が更新します。 - ステアリング機能
→計算状況を見ながら、途中で停止・条件変更・再開可能です。 - プローブ機能
→画面上の3次元図形をマウスでクリックして解析結果の情報表示できます。 - 時系列グラフ・空間分布グラフ表示
→ヒステリシスループ・ジュール熱・マックウェル応力・トルクなどのグラフ化できます。
信頼性
透明性が重要
ソルバーはブラックボックスではなく透明性の高いものが信頼の証拠となります。
- テキストベースの入出力ファイル1つでリスタート
→データの互換性・可搬性・可読性・再利用性・加工性
→解析ソフトウェアとしては信頼性を示す重要な要素の一つである入出力データの透明性
- XML,CSVファイル形式の結果のエクスポート機能
- 再入可能な入出力ファイル形式
→出力ファイルをそのまま入力にできる階層的ファイルフォーマット
→リスタート計算・分岐リスタートが簡単
→オリジナルファイルフォーマットはFORTRANなどで読み込み易いフリーフォーマット
解析というより実験に近い直感的な使用感
直感的な入力条件で磁場設計スキルの向上に
- 数値解析特有の難しい入力が非常に少ないです。
→境界条件・ゲージ条件・電流密度への換算等々は不要です。
- 入力データは製品を作るときに必要な直接的なパラメータが中心
例 各部寸法・B-H曲線・電流のアンペアターン値
→数値解析特有の知識はあまり要りません。
→試作物を作るような感覚でモデルを作ることができます。
→磁場製品を作る知識の方がより重要で、製造設計スキルの直接的な感覚が研ぎ澄まされます。 - セル(要素)を重ねることにより物性の重複を表現できます。
- 複雑なコイルの巻き方 (サンプルあり)をしていても正確にモデル化できます。
さらなるQmの利点 -他の解析法との違い
Qmの解析手法は?
Qmの利点を定量的に示すため、以降の節では以下について順に説明します。
- 磁場解析法の種類
- FEMの3次元磁場解析には呪いに等しい落とし穴が・・・
- その前に確認事項
- 3次元磁場解析とFEM
- 2次元と3次元計算量の比較
- 計算ループにおける精度
- 計算ループとQmの解析コントロールパネル
- 磁場超越関数(電流の場合)
- 磁場超越関数(磁性体の場合)
- 面変数型磁気モーメント法
磁場解析法の種類
Qmは積分方程式法の一つである、「面変数の改良型磁気モーメント法」になります。
解析は(モンテカルロ法などを使わない限り)実験と違って、いわゆる計算誤差以外の統計学的誤差はありません。 実験値との差を理論誤差という場合がありますが、元々解く問題を近似したり、プロセスを省略、仮定したのだから、 近似による差あるいは理論による食い違いというべきでしょう。 もちろん、比較するとき実験値の方の実験誤差は考慮しなければなりません。
理論解析法
理論解析値(Theoretial Analysis Value)を求める方法です。 理論解析値は、理論式から直接的・間接的に求めます。
計算にコンピュータを利用するしても、電卓的利用から、複雑な積分値の計算まで長時間要するものもあります。 シミュレーションと大きく違うのは、初期段階に於いてモデルの離散化というものが無い点です。 空間的には理想的な形状を仮定したり、物性値の分布に平均値的なモノを利用します。 いわゆる集中定数系(一点モデル)として扱うことが多いのが特長です。 コンピュータによるシミュレーションができなかった時代には、様々な経験式とともに、様々な理論が現実のモデルの近似値として扱われていまいした。 今でも、電気回路と伴に磁場解析を行う場合に利用されます。
従いまして、集中定数の簡易計算法であったり、解析解が得られる限られたもので使えません。 具体例として以下のような手法があります。
・複素数を利用した等角写像
・磁気回路法
・パーミアンス法
微分方程式法
コンピュータでシミュレーションとして汎用的な電磁界解析する場合は、マックスウェルの方程式から出発し、それに様々な離散化手法を駆使し、現実問題を解くものです。 離散化の過程でマックスウェルの方程式の微分的表現から出発したものを微分方程式法と呼ばれます。
- 差分法 → メッシュが等間隔
メッシュに分割するのですが、一定の間隔(等差間隔)、または等比間隔(対数的に等差間隔)で空間や時間を分割する方法です。 また、その式の解き方により、陽解法と陰解法に別れます。 空間的に有限要素法や積分方程式法を用いても、時間的には差分法で解くことが多いです。 - 有限要素法(FEM) → メッシュが矩形出なくても良い
微分方程式法の代表格です。 有限要素法は、世界的に学会および産業界でも広く研究・利用され多くの論文や理論が発表されています。 他社の磁場解析と言えばほとんどがこの手法です。 中でも辺要素有限要素法は有名で、市販の多くのプログラムにも採用されています。
変数の取り方で以下のような分類があります。
・スカラーポテンシャル法
・A-Φ法
・T-Ω法
積分方程式法
マックスウェルの方程式の積分的表現から出発したものを積分方程式と呼ばれます。 グリーン関数という積分核を持つ積分を計算します。
- 境界要素法(BEM) →非線形が扱えない
モデルの表面のみ分割する方法です。 メッシュ分割は簡単で、計算も速いのですが、モデル内部に湧き出し・消滅がある問題は解くことができません。
つまり、同じ物性でも解となる場の関数になるような非線形性がある場合、内部に湧き出し・消滅がありますので適用できないと考えてください。 ただし、積分法ですので重ねあわせがきき、局部的なモデルの解法として利用することができます。
電磁場解析の場合、強磁性体は一般的に B-H曲線を持った非線形性を有しますので、BEMだけで解くのはかなりの近似といえましょう。
それに対して、静電場解析のようなものは、 導体と誘電体(ほとんど非線形性がない)のみですので、かなり有効的に利用できます。 - 磁気モーメント法(IEM)
BEMの欠点である非線形性を考慮するため、モデル内部までメッシュ分割する方法です。 実は、有限要素法が成功するかなり前のコンピュータ黎明期からこの手法は用いられてきました。 しかし、通常の磁気モーメントと言われる磁気双極子をそのまま扱った方法では、空間メッシュが無いとは言え、磁性体を磁区のように細かく分割しないと積分の精度が得られず、頓挫していました。 - Qmは「面変数の改良型磁気モーメント法」
弊社ソルバーQmは磁気モーメントですが改良がなされています。 BEMの場合もそうなのですが、この方法を成功させるには、粗いメッシュもでも積分法を精度よく、効率良く行う必要があります。
Qmでは、面に変数を置くことによりこの問題を解決しています。 磁気モーメントという呼び名は 磁石などの磁性を示す単純なベクトル的イメージがどうしてもまとい付くのですが、実際の磁性体は細かい磁区が分布しているのであるので巨視的にどのように振る舞うか、そのことを良く考えて、理論計算モデルを作成する必要があります。
さらに、Qmでは、渦電流解析を電流ベクトルポテンシャルと双対原理を使い、より進んだ「面変数の改良型磁気モーメント法」として統一的に取り扱って解析に成功しています。
FEMの3次元磁場解析には呪いに等しい落とし穴が・・・
磁場解析にもFEMが多用される理由
一般に利用されている磁場解析ソフトは有限要素法(FEM)によるものがほとんど
→構造解析で大成功を収めた。
→FEMライブラリ・ノウハウが蓄積。
→非構造(流体・磁場・音場)解析への適用 連成計算目的。
2次元磁場解析のFEM(ベクトルポテンシャル法)で成功。
★しかし 磁場の現象はそもそも空間的に3次元である。
・・・FEMの3次元磁場解析には呪いと言っていいほどの落とし穴が・・
3次元磁場解析は必要不可欠
2次元磁場解析には限界があり、3次元磁場解析の要請は次のようなものから来きます。
電流と磁場との関係は元々3次元でしか表せない
→次元を減らしたために不可解な補正項が出現。
→かえって問題を複雑化・精度を損なう。
解析対象は重厚長大から小型・薄型軽量へ
→表面積/体積 比が大きくなる
→磁場が横から漏れやすい
→エネルギーロス発生
→定格出力を得るため電流値を大きく
→低電圧化によりさらに電流値が大きく
→狭い空間に大きな電流とロス
→発熱
→悪影響、熱ににより磁性体の透磁率が下がると性能が落ちる。
→ロスを少なくするため、3次元的に磁路を確保し設計する。 磁場がどう流れるか3次元磁場解析が必要。
3次元磁場解析は難しい
2次元計算より細かいメッシュが必要
3次元解析では、針のような形状の計算があり、非常に鋭い空間磁場のピークが出る。 理論的には、関数系は超越関数になる。
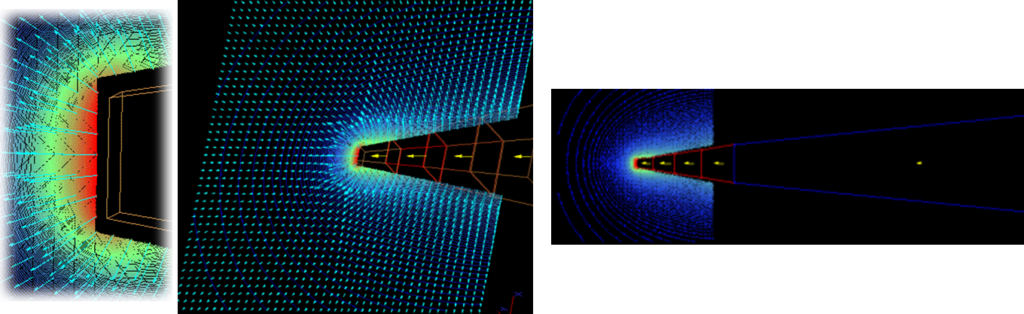
Qmによる解析 先端に磁場が集中
解析例はQmのものです。
余り鋭くない くさび型の磁性体の解析ですが、これでも先端部分はかなりの磁場が集中し、大きな変化が見られます。 先端に4つの鉄の磁性体セル、太い部分は一つ永久磁石のセルです。 粗いセルブロックでモデル化していますが、先端部の鋭い磁場を精度良く計算できています。 精度が良いのは、Qmは超越関数を直接積分して計算しているからです。
磁気ヘッド、磁気記録製品は尖った先端に磁場が集中するこの性質を利用して記録密度を上げています。 プランジャ・モータ等でも極の形状の3次元的磁束集中が性能を左右します。
3次元磁場解析とFEMとは相性が良くない
急激な磁場変化を3次元で正確に計算する必要があります。
FEMは磁場(ベクトルポテンシャル)をメッシュ間の収支バランスで解く
→メッシュ内部は、求める場が形状関数(補間関数)で表され、その関数系は初等関数
→初等関数は冪上の多項式であるが実際には一次式・二次式までに限られています。
→しかし、磁場の関数は、急激な変化が特長の超越関数です。
急激な変化を正確にとらえるためには、2次元解析以上に細かい空間メッシュ分割が必要です。
→周りのメッシュ引きずられて細かくする必要があります。
3次元解析が理想だが、敬遠される理由
→高次元解析は取り扱う変数の数が幾何級数的に増えます。
→計算量はさらにその3乗倍になります。
→高パワーの計算機・プリポスト・ソルバー →高額になります。
Qmは、FEMなどと比べて3次元解析が得意です。


