第二部 何故 3次元磁場解析はQmが有利なのか!
目次
計算量の比較
ここで、ほとんどの磁場解析で用いられているFEM(有限要素法)における計算量の見積をしてみます。
2次元と3次元でのFEMにおける演算量
単純にするため1メッシュ1変数としてまず見積ってみます。
2次元の場合
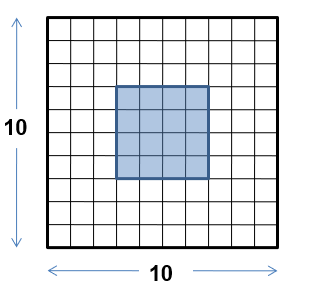
・10×10のメッシュ 100変数
・マトリックスサイズの見積
\(\mathbf{N=100}\) バンド幅 \(\mathbf{W=10}\)
・演算量 \(\mathbf{CPT2D = N × W^2}\)
\(\mathbf{CPT2D =100 × 10^2 = 10^4}\)
3次元の場合
上記を3次元モデルに拡張してみます。
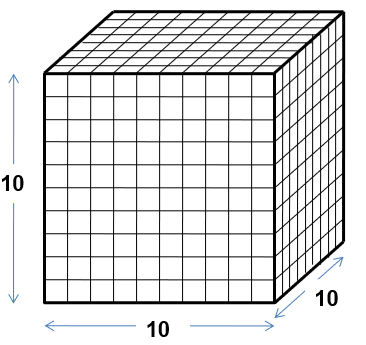
・10×10×10 のメッシュ 1000変数
・マトリックスサイズの見積
\(\mathbf{N=1000}\) バンド幅 \(\mathbf{W=100}\)
・演算量 \(\mathbf{CPT3D = N × W^2}\)
\(\mathbf{CPT3D = 1000 × 100^2 = 10^7}\)
・演算量の比
\(\mathbf{\cfrac{CPT3D}{CPT2D} = \cfrac{10^7}{10^4} = 10^3}\)
3次元にすると待てど暮らせど・・・
・計算量の比 \(10^3\) の意味するもの
2次元計算で 1秒で終わる計算が
3次元計算では 1,000秒 ≒ 16.7分 かかる
一辺が100であれば 計算量の比は \(100^3 = 10^6\)
2次元計算で1秒で終わっても
3次元計算では \(10^6\)秒 ≒ 277.8時間 ≒ 11.6日
ところが、磁場解析ではベクトル量なのでもう少し計算量が増えます。
2次元はスカラーポテンシャルで1メッシュ1変数
3次元は 3成分(ベクトルポテンシャル) なので変数の量は 3倍となります。
計算量の比は \(300^3 = 3^3×10^6=27×10^6\)
\(27X10^6 秒 = 312.5日\)
FEMのように、空間含めたメッシュ分割を必要のある手法は、次元解析ではコストが非常に高い
しかしこれはガウスの消去法を使用した場合の話でICCG法などそれに準じた強力な手法があるというが・・・
非線形が標準の磁場解析では、実はそうではない。
ICCG法などでは精度を落として計算時間を短くしているだけで、線形計算の場合はある程度精度の保証ができるが、非線形計算ではそうは行かない。
前段で精度を落とすと、むしろ後段での非線形の収束計算で時間がかかることになり、最悪の場合は、収束せず(有意な買いが得られない)ということもあります。
その状況を示すと次のようになります。
マトリックスソルバーの精度を落とすとツケが後にくる
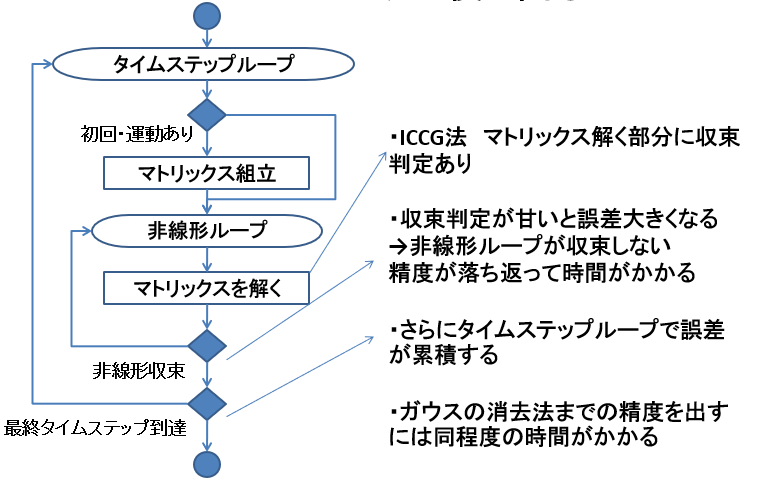
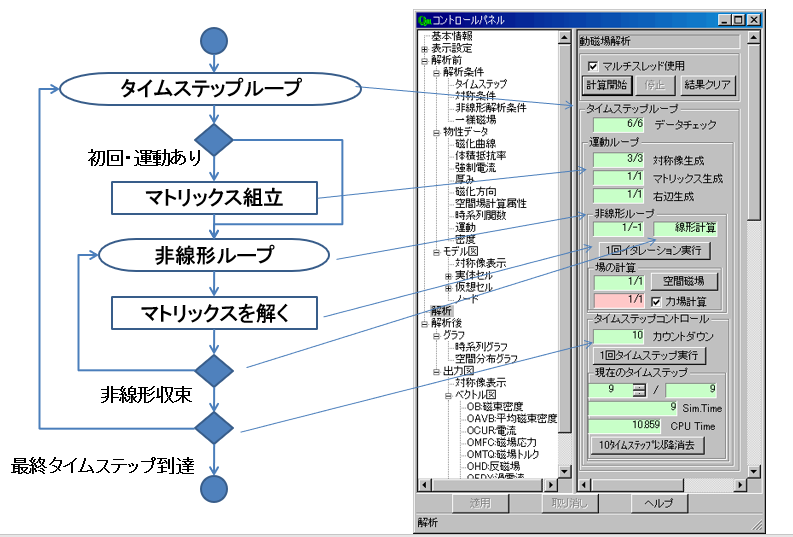
Qmの解析コントロールパネル
Qmの解析コントロールパネルでは前述の非線形収束計算を含めた計算状況をリアルタイムに可視化しています。
磁場解析は他のCAEの分野より精度の要求が厳しい・・・
磁気の利用は古くから歴史があり、経験的にわかっていることが多く、その利用に関して多くの知見があります。
また、物理的にも電磁気の範疇であるため、工学では応用・実用範囲においても力学の摩擦・座屈・流体などと違い再現性が高く精度よく定量的に測定でき、産業革命以降、既に世界中に多くの利用機器があります。
・実測しやすい。 経験・実用例が多岐にわたり、高精度の計測器がある。
・物理現象の取り違えがければ、合って当たり前の世界。
→理論解を求めやすいモデル・実験・シミュレーションが可能なものが多い。
・磁場の値そのものよりも応力やトルクなど二次結果を求めることが多い。
→力に換算すると誤差が大きくなる。 後述。
・特に非線形計算を途中で打ち切ると磁気飽和が正確に計算されない。
→磁気飽和を起こすような磁束密度が強い部分は、ボトルネックに なっていてその系の磁路を支配することが多い。
・上記の事情があり、コンピュータが普及してからの他のCAEの分野とも異なり、元々、精度の要求が厳しい。
力に換算すると誤差が大きくなる例
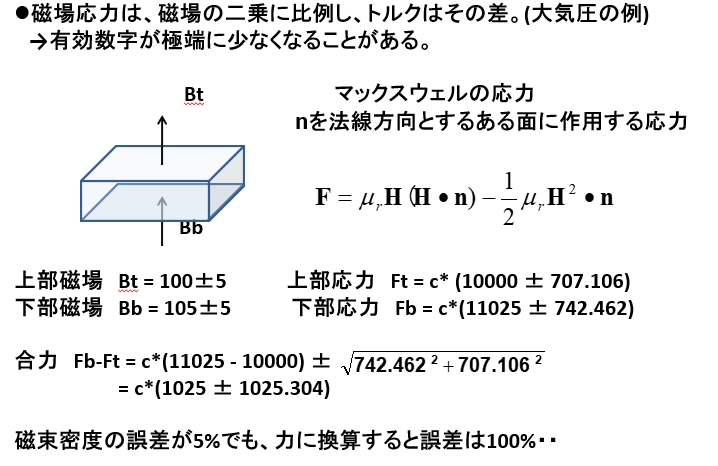
以上の話は大気圧に関するものでもよく知られています。
磁場・磁束密度を表す関数は急激に変化する超越関数
本来、磁場や磁束密度は空間的に急激に変化する超越関数であることが知られています。
単純な矩形コイル近傍の磁場をビオサバールの法則で計算することにより、如何に磁場が空間上で本質的に急激な変化をすること示すことができます。
単純な矩形コイル近傍の磁場
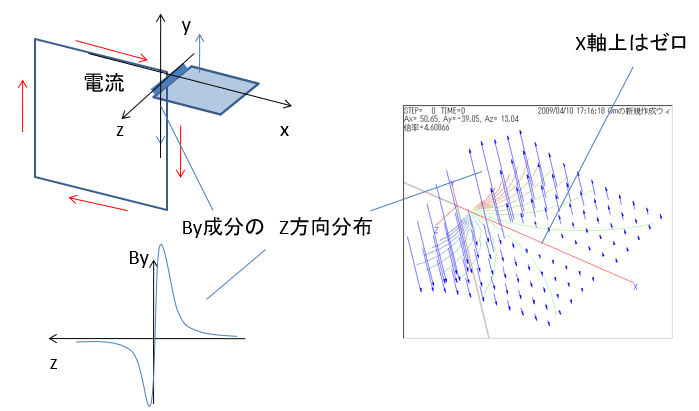
左図のZ軸上の 空間磁場は 電線の半径が 0 で電流密度が +∞とすると
Z = -∞ → 0 のとき By = 0 → +∞
Z = 0 のとき By = 0
Z = 0 → +∞ のとき By = -∞ → 0
なります。
実際には、電線の半径は有限ですが、非常に電流密度が高いものは簡単に現れます。 従いまして、青い平面のコイル寄りの太い青い線上の By 成分は Z=0 つまりX軸上の By 成分は0に近いのですが X軸から少しずれると大きな値を取ります。 この急激な変化は、結構広範囲の空間にわたって、影響を与えます。
つまり、超越関数は尖っていて、FEMで表現しようとすると非常に細かい空間メッシュが必要です。
FEMではメッシュ間のバランスで計算が成立しているため、急激にメッシュを小さくすることはできません。
そもそも、FEMの原理となっている変分原理は、初等関数で成立するもので超越関数では成り立ちません。 ※微妙にガラーキン法で何とかなると言うレベルで、高精度とは言い難い代物です。
FEMは、構造解析など応力などが初等関数で表されることが前提で利用された手法ですので、特に三次元磁場解析のように急激に変化する補完関数(形状関数とも言う)は想定外なのです。
また、磁気を使う磁気記録製品や機器は、この尖りを利用して、記録密度を上げたり、モータではトルクを稼いだりしています。 この尖りの部分は、非線形性も強く磁気回路全体のボトルネックにもなり、製品の性能を左右しますので、精度良く解析するのは非常に重要なのです。
Qmではビオサバールの法則(Biot-Svart low)をそのまま計算しますので離散化誤差は最小限に押えることができます。
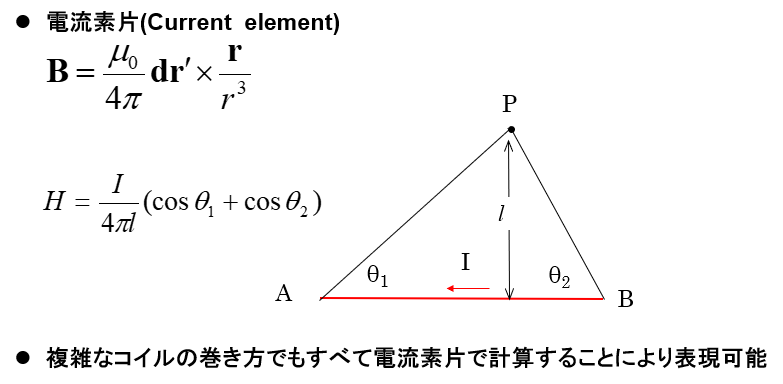
ビオサバールの式から、解析的に計算できます。
式を見れば分かるますように、解析解には超越関数 と呼ばれる三角関数が現れます。
これは、FEMが採用するべき関数では多くの項をとっても近似度が劣化することが知られています。
Qmではビオサバールの式そのものを使用していますので精度は保たれます。 また、曲線を表現するため、細かい素片に分割しても、空間メッシュが必要ないため計算負荷はほとんどかかりません。
Qmの面変数型磁気モーメント法では解析解を使って計算
先の例は、Qmが採用している電流による磁場計算を解析解を使って解く例でした。
磁性体に於いてもQmは、磁性体面の面磁荷を解析積分することにより、疎分割でも高精度を実現しています。
磁性体の内部の磁束密度は比較的変化が少なく、一つの磁性体面での面磁荷密度の変化もほとんどありません。※1
しかし、磁性体近傍の空間における磁場は、急激な変化を起こします。 これは、電流におけるビオサバールの法則の計算と同じように、積分の効果が原因ですので、その面積分の解析解を使えば良いという仕組みです。
Qmでは、磁性体の面に対して変数(面磁荷密度)を置いて十分な精度を得ています。
このように、面に変数を置く改良型磁気モーメント法を、弊社では「面変数型磁気モーメント法」と呼んでいます。
下図は面磁荷密度が一定として計算しても、面の縁で空間磁場の急激な変化を表現できていることを示した図です。

図はでは 直方体の磁石セル一に対しては、一つの変数で計算できます。 なぜなら、面変数としてはたった一つのスカラー変数で(N極とS極の値は総量同じ値になるため一つで)よいからです。 解析的な面積分により、面近傍の空間磁束密度の連続的な細かな変化が計算されている様子が分かります。
※1 ただし、他の磁性体が面に接続していたり、面に近づいたりするような場合は、面磁荷密度が変化しますので次ページのような取り扱いが必要です。
更新日
現在構築中

